Method validation
Prior to introducing a new, unknown method, every conscientious analyst will first carry out its validation. This is done out of professional conscience and aspiration to provide reliable measurement results, i.e. results on which the right decisions can be made. In line with the definition from the new vocabulary in metrology VIM 3 (1), a validation of an item (e.g. of a measurement procedure, method) means provision of objective evidence that a given item fulfils specified requirements, where the specified requirements are adequate for an intended use. Objective evidence means records of having carried out validation experiments.
Method performance characteristics and related acceptance criteria
Validation experiments spend time and money and therefore it is exceedingly important to plan them well. There are two highly critical steps in this particular planning:
- recognizing significant method performance characteristics for a stated usage of a method; and
- setting requirements (criteria) to these characteristics, and yet again keeping in mind the stated usage of a method.
Method performance characteristics are as follows:
- linearity (measurement area);
- measurement precision:
- measurement repeatability - precision under the repeatability condition of measurement – same analyst, same sample, same measuring system, same operating conditions, same location, short period of time (frequently used term for this concept in clinical chemistry and laboratory medicine is intra-assay precision);
- intermediate precision – precision which is achieved within the same laboratory over an extended period of time but may include other conditions involving changes: new calibrations, calibrators, operators, and measuring systems;
- measurement reproducibility - precision under the reproducibility condition - precision which is reached between laboratories (it is usually not quantified in case of in-house method validation, but it is an important parameter in method standardization);
- measurement trueness:
- bias (b) and/or recovery;
- selectivity;
- limits of detection;
- limits of quantification;
- method robustness.
It is not necessary to test all performance characteristics for each usage of the method. For instance, in methods where the task is to discover weather something exists in the sample or not, the analysts will most probably be interested in the limits of detection and selectivity. If they have to determine the cause (identification), selectivity will be of critical significance. But, when they have to issue a quantitative result, all the above stated method performance characteristics become interesting, except for the limits of detection. The frequently used slogan whereby the scope of validation is a compromise of costs and risks does not pertain to the selection of performance characteristics, but only to the number and scope of experiments to be estimated.
In real life, most problems for laboratories are posed by setting the acceptance criteria to method performance characteristics, not by their selection. The criteria should be set before carrying out validation experiments, keeping in mind the ability to interpret results thus obtained, i.e. making the right decisions based on these results. Unfortunately, in most cases the criteria are set based on results obtained through validation experiments. The statement written at the end of the validation stating that the method complies with a particular usage makes no sense then.
Target measurement uncertainty and acceptance criteria
When a result is quantitative, the user’s request will be its accuracy. In quantitative terms, this request is described with target measurement uncertainty which represents the greatest allowed uncertainty for a particular usage of that result. Since measurement uncertainty encompasses all random and non-corrected systematic errors, it is understandable that the target measurement uncertainty will impact the defining of criteria to characteristics such as measurement repeatability, intermediate precision, reproducibility, bias and/or recovery.
Measurement uncertainty
Measurement uncertainty is estimated in line with the internationally and multidisciplinary harmonized Guide to the Expression of Uncertainty in Measurement (GUM) (2) issued in 1993, corrected in 1995. The following international organizations participated in its assembly: Bureau international des poids et mesures (BIPM), International Electrotechnical Commission (IEC), International Federation of Clinical Chemistry (IFCC), International Organization for Standardization (ISO), International Union of Pure and Applied Chemistry (IUPAC), International Union for Pure and Applied Physics (IUPAP) and International Organization of Legal Metrology (OIML).
According to GUM, each uncertainty component is quantified by an estimated standard deviation, called, for this purpose - standard uncertainty. GUM describes two ways of evaluation – type A, estimated by statistical means, and type B, estimated by other means.
Type A standard uncertainties are obtained as a standard deviation (of the mean) of replicate measurements, or as a standard deviation from the fit of a calibration curve, characteristic standard deviation from a control chart etc.
Examples of uncertainty sources evaluated by type B evaluation are: manufacturer’s quoted error bounds for a measuring instrument, interval of values of measurement standards, data from calibration report etc. Despite the fact that type B uncertainties are essentially based on scientific judgement and are therefore subjective and personal, the reliability of some uncertainty estimate does not depend on the way of evaluation, but exclusively on the quality of information which was basis for evaluation.
Combined standard uncertainty is obtained using the “root-sum-of-squares” method. All standard uncertainties thereat are equally mathematically treated, regardless if they were obtained through type A or B evaluations. The result is usually reported with expanded uncertainty which is the multiplication of combined standard uncertainty of result and factor k which ensures the agreed coverage probability, usually P = 95 %.
Measurement uncertainty is still relatively misunderstood in many areas of measurement and so in the field of medical biochemistry. However, as the evaluation of measurement uncertainty is one of the requirements of ISO 15189, is increasingly accepted that in addition to the method performance characteristics can be one of the quality indicators (3).
How to include data from validation experiments into measurement uncertainty estimation?
Measurement uncertainty is a property of measurement result, not of the method, equipment or laboratory and therefore it is to be expected that it is assessed only once the result is obtained. If the main sources of error would be within the measurement (or testing) process itself, and not for instance caused by a non-homogenous sample, it is possible to make a satisfactory measurement uncertainty estimation using method performance characteristics like precision and trueness estimates. Initial information on this method performance characteristics are obtained by performing validation experiments.
Random errors are estimated via precision experiments and represented as standard deviations (s) or coefficients of variation (CV). Out of the three precision levels mentioned (repeatability, intermediate precision and reproducibility), the most interesting one in measurement uncertainty assessment (made from validation experiments) is intermediate precision since it includes much wider sources of random errors than it would be the case with repeatability. Reproducibility is not established in an in-house validation.
Trueness, which is expressed in terms of bias (b), is investigated by comparing the expected reference value (xref) with the estimation of the result given by the method (x):
b = x̄ – xref
Reference value is most commonly the value of certified reference material (CRM) determined with the appropriately low measurement uncertainty and with documented metrological traceability. Reference material should have a matrix as close as possible to the matrix of the material subjected to measurement. Bias could also be determined using another method of higher metrological order, but this is rarely possible in real life.
Case 1: uncertainty when correction is applied
A prerequisite for the GUM is that “the result of a measurement has been corrected for all recognized significant systematic effects”. In such a situation the result of measurement (ykor) is reported as:
ykor = y – b.
To make correction technically feasible and justified, the estimate of bias (b) should be sufficiently accurate, well established, and significant in size. Then only the uncertainty of correction ub enters into the calculation of uncertainty:
where:
s(x̄) is experimental standard deviation of the mean x̄, given by:
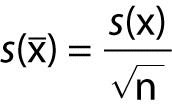 .
.s(x̄) is experimental standard deviation of response of the method to a reference material with the known value assigned to the material (xref).
n is the number of observations made in this trueness experiment.
u(xref) is measurement uncertainty associated with the quantity value of a reference material (type B evaluation GUM (2)).
If contribution of random errors is added (precision s), then the measurement uncertainty of the corrected result is:
where:
s is standard deviation obtained from intermediate precision experiment.
ub is a component of uncertainty due to estimation of bias.
Sometimes to this uncertainty some other of its components should be added. Examples of such components are contribution of sampling effects, sample preparation, sample inhomogenity etc. The result is reported as:
Y = ykor ± ku(ykor).
When normal distribution is assumed, coverage factor k is equal to 2.
2.Case: Uncertainty when correction is not applied
Although GUM (2) strongly recommends the correction of reported results of measurement with a known systematic effect (b), in some cases it might not be practical and feasible or might be too expensive. The correction of results may require modifications to existing software and “paper and pencil” corrections can be time consuming and prone to error. In such very special circumstances when a known correction b for systematic effect cannot be applied, the “uncertainty” assigned to the result can be enlarged by it. Several methods could be applied for this. GUM (1) describes a method when such enlarged “uncertainty” is the sum of expanded uncertainty and a known systematic effect (b). The measurement result is reported as:
Y = y ± (ku(ykor) + IbI).
Eurolab document (4) gives a method where a known systematic effect (b) is treated as an uncertainty component:
The measurement result is reported as:
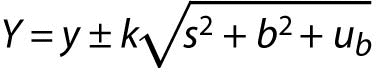 .
.There are some other suggested methods for reporting the uncertainty. Laboratories should choose the one that can be easily interpreted by the user and that will not give a wrong insight into the magnitude of the uncertainty of measurement. E.g. the method of reporting described in Eurolab document (4) is not appropriate when b>>s.
The accuracy of measurement uncertainty estimation
The scope of validation is a compromise of risks and costs, so the extent of experiments results from this compromise. This is most prominent in the determination of intermediate precision. In order for a laboratory to get a good approximation of intermediate precision, it has to recognize the factors which will cause errors in measurement and simulate them in the course of validation. In practice, the change of two factors is applied most frequently: staff and time, meaning the repetition in measurement is usually done by different personnel over the course of several days. Later, it is regularly proven that actual precision is a great deal lower than determined by validation experiments.
Consequently, when measurement uncertainty is assessed on the basis of information on method performance characteristics, it is important to ensure permanent statistic monitoring. This monitoring proves the reality of estimation of the method performance characteristics, and thereby also the validity of measurement uncertainty estimation and recognizing the changes thereof.
Besides for internal quality control measures, it is important to regularly participate in inter-laboratory testing since sometimes it is the only way to discover systematic effects undetected in a laboratory.
Conclusion
Measurement uncertainty is a property of measurement result, not of the method, i.e. of the testing/measurement process. Assuming that the testing/measurement process is the chief source of uncertainty, it is possible to estimate measurement uncertainty on the grounds of its performance characteristics. The first information thereof is obtained through validation experiments. Afterwards, it is essential to monitor their performance characteristics in order to prove the validity of assessment. Should it be noticed that the performance characteristics have changed, it is necessary to update the assessment with new data.
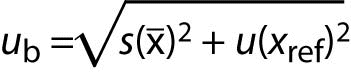
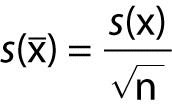 .
.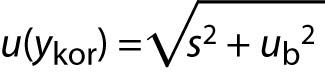
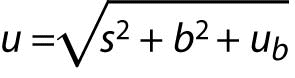
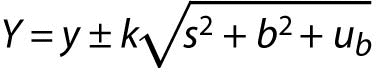 .
.

